Open Channel Flow

Think about a river flowing downstream or water running through an irrigation ditch after rain. You’ve seen water in open channels your whole life, but you probably didn’t realize they’re fundamentally different from water flowing through pipes.

In a pipe, water gets pushed by pressure and fills the whole thing. It’s enclosed, it’s under pressure, it’s basically trapped. But in an open channel like a river or canal, water just flows downhill because gravity is pulling it. One surface is open to the air. That’s the key difference, and it changes everything about how the water behaves.

What is Open Channel Flow?

Open channel flow is the movement of water through a channel where at least one surface (the top) is exposed to atmospheric pressure. The driving force is gravity, not pressure from a pump or reservoir above. Water flows downhill because it’s pulled by gravity, not pushed by pressure.

A. Fundamental Flow Classifications

Critical Flow represents a unique equilibrium state where specific energy reaches its minimum value. At this condition, the Froude number equals exactly one, marking the boundary between two fundamentally different flow behaviors. Critical depth depends solely on discharge rate and channel geometry, independent of slope or roughness.

Subcritical Flow characterizes deeper, slower-moving water typical of rivers, large canals, and low-gradient channels. With a Froude number less than one, this tranquil flow regime exhibits downstream control, meaning conditions further along the channel influence upstream behavior. This makes subcritical flow relatively predictable and manageable through channel transitions and modifications.

Supercritical Flow develops in steep channels where water moves rapidly at shallow depths. The Froude number exceeds one, and upstream conditions control the flow. This rapid flow creates challenges including violent wave action, difficulty in changing flow direction, and potential erosion issues. Supercritical flow commonly occurs in mountain streams, spillways, and steep drainage channels.

B. Key Hydraulic Parameters

Hydraulic Radius

is one of the most important geometric properties in open channel flow. It’s defined as the cross-sectional area of flow divided by the wetted perimeter:

where:
A = flow area
P = wetted perimeter

The hydraulic radius represents the efficiency of the channel cross-section. A circular pipe flowing full has the maximum hydraulic radius for a given area, making it the most efficient shape.

Hydraulic Mean Depth

Also called hydraulic depth,

Boundary Shearing Stress

represents the force per unit area that flowing water exerts on the channel bed and sides. This stress is what causes erosion and sediment transport. For uniform flow in a channel, the boundary shear stress can be calculated as:

Where:
= Boundary Shear Stress
R = Hydraulic Radius
S = Slope of energy radiant

The concept of boundary shear stress connects directly to permissible velocities in channel design. Materials with higher resistance to shear stress can withstand higher flow velocities without eroding.

C. Uniform Flow

1. Manning’s Equation

Manning Equation is the foundation of Open Channel Analysis. It relate the velocity to channel properties.

where:
A = cross-sectional area of water
V = velocity from Manning’s equation

D. Chézy’s Formula: The Foundation

Before Manning’s Equation became the standard, Chezy’s formula was the primary method for analyzing open channel flow, and its significance remains in hydraulic engineering.

where:
V = mean velocity
C = Chézy coefficient
R = hydraulic radius
S = Channel Slope

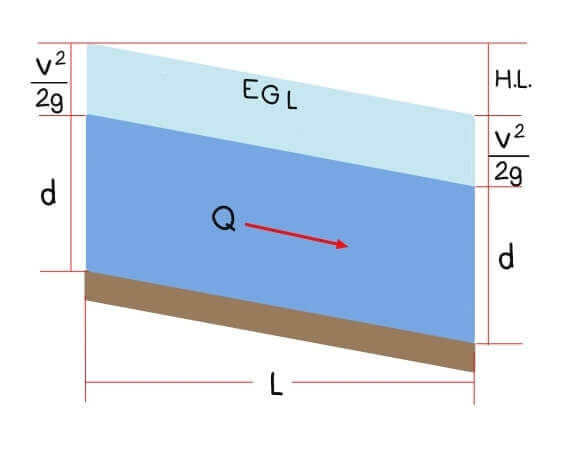
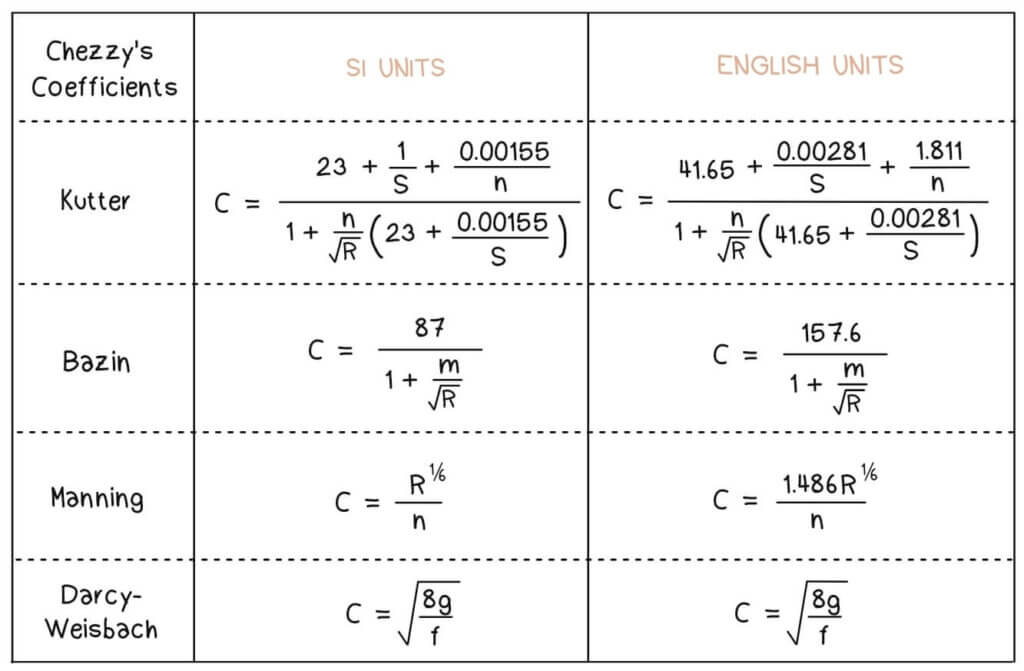
Table for Chezy’s Coefficients (C) using other formula

E. Energy Analysis in Open Channels

Specific Energy

Specific energy represents the energy content measured relative to the channel bottom, combining depth with velocity head (V²/2g). This concept proves invaluable for analyzing flow transitions, computing critical depth, and understanding channel behavior.

For any given discharge in a specific channel, plotting specific energy against depth produces a characteristic curve with a minimum point. This minimum corresponds to critical depth—the most efficient depth for conveying that particular discharge.

Total Energy and the Energy Equation

Total energy includes specific energy plus the elevation of the channel bottom above a reference datum. The energy equation (Bernoulli’s equation adapted for open channel flow) tracks energy changes between channel sections:

F. Critical Depth and its Significance

The general equation for determining critical depth:

where:
g = acceleration due to gravity
A = cross-sectional area
T = top width of water surface

Froude Number

The Froude number offers a dimensionless parameter for flow classification:

Fr > 1.0: Supercritical flow
Fr = 1.0: Critical flow
Fr < 1.0: Subcritical flow

Conclusion

Open channel flow seems simple on the surface, water flowing downhill. But the physics is significant and the applications are everywhere. From the irrigation canal bringing water to crops, or even analyzing environment the behaviour of storm rain that flows up there in the mountain to the city down below, the open channel flow principles are at work.

Whether you’re designing a channel, predicting flood depths, or managing water resources, understanding how gravity, friction, depth, and velocity interact is essential. Manning’s equation gives you the tools to predict behavior. Recognizing subcritical and supercritical flow helps you understand what will happen when water encounters obstacles or slope changes.

References:

Chaudhry, M. H. (2008.). Open-Channel Flow (2nd ed.).

Davidian, Jacob. (1984). Computation of water-surface profiles in open channels (No. Techniques of Water-Resources Investigations, Book 3, Chapter A15). https://doi.org/10.3133/twri03A15