Most Efficient Sections in Open Channel

Most Efficient Section

In hydraulic engineering, efficiency isn’t just about doing things faster or cheaper. It’s about designing channels that move water with minimal resistance, require less excavation, and use materials wisely.

Understanding the Most Efficient Sections in Open Channel can significantly enhance the performance of hydraulic designs.

What you’ll learn

What Makes a Channel Section Efficient?

An efficient channel section is one that delivers the maximum discharge (flow rate) with the minimum wetted perimeter for a given cross-sectional area. Why does this matter? Because the wetted perimeter is where friction happens, it’s where the flowing water rubs against the channel walls and bed, losing energy in the process.

Think of it this way: if you had to move a certain volume of water from point A to point B, would you rather use a channel that requires less concrete lining, less excavation, and less maintenance while still delivering the same amount of water? That’s what efficiency is all about. It’s the hydraulic engineer’s version of getting more miles per gallon.

Fundamental Equations

The discharge in an open channel is governed by Manning’s Equation:

$Q =\frac{A}{n}R^{2/3}S^{1/2}$

Where:
Q = discharge (flow rate)
A = cross-sectional area
n = Manning’s roughness coefficient
R = hydraulic radius
S = channel slope

The hydraulic radius is defined as:

$R=\frac{A}{P}$

Where P is the wetted perimeter

For maximum efficiency at a given area, we need to minimize the wetted perimeter P, which maximizes the hydraulic radius R and consequently the discharge Q.

Overview of the Formulas

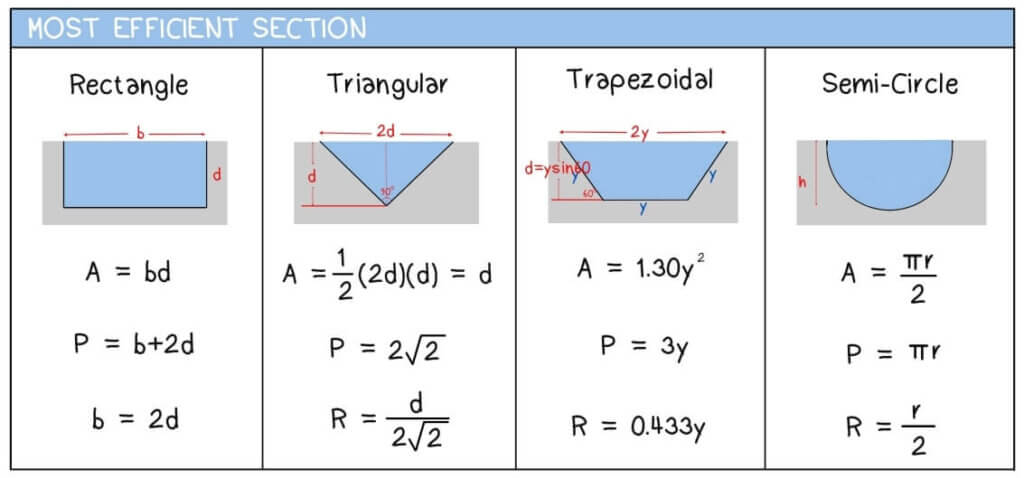
1. Rectangular Section

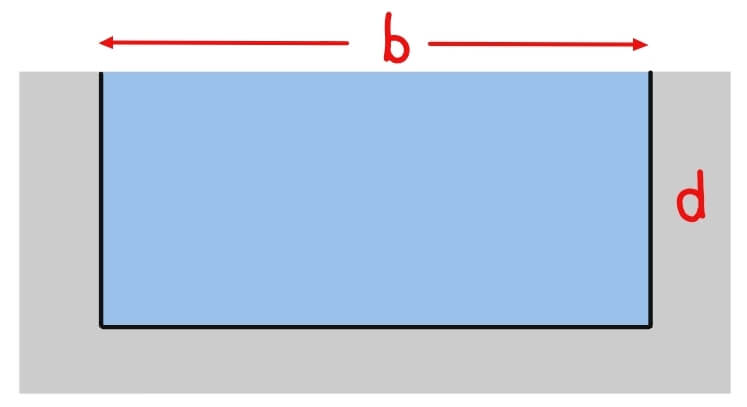
Area:

$A=bd$

Perimeter:

$P=b+2d$

Deriving the Most-Efficient Dimension
Expressing the perimeter in terms of area and depth:

$P=\frac{A}{d}+2d$

To minimize P, we take the derivative with respect to d and set it equal to zero:

$\frac{dP}{dd}=-\frac{A}{d^2}+2$

Solving for the relationship between b and d:

$\frac{A}{d^2}=2$

$\frac{bd}{d^2}=2$

$b=2d$

The most efficient rectangular channel has a width equal to twice its depth (b = 2d).

2. Triangular Section

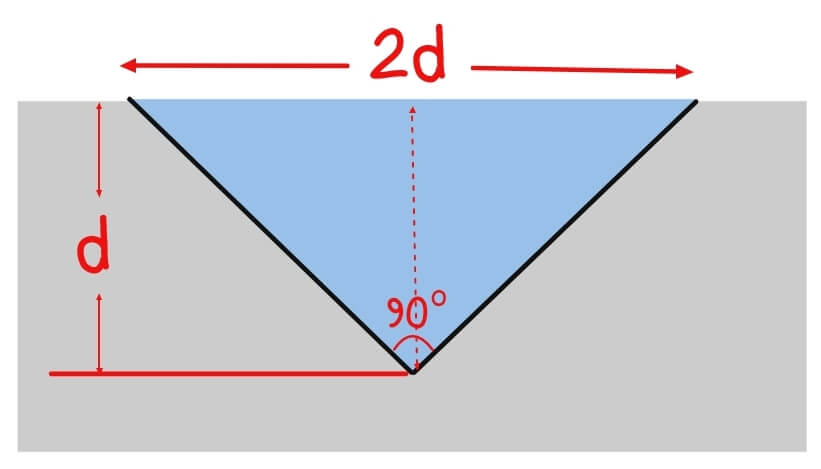
For a triangular channel with side slope angle and vertical depth d:

Area:

$A=\frac{1}{2}(2d)(d)=d^$

Perimeter:

$P=2\sqrt{d^2+d^2}=2\sqrt{2}d$

This hydraulic radius can be expressed as:

$R= \frac{A}{P}=\frac{d^2}{2\sqrt{2}d}=\frac{d}{2\sqrt{2}}$

3. Trapezoidal Section

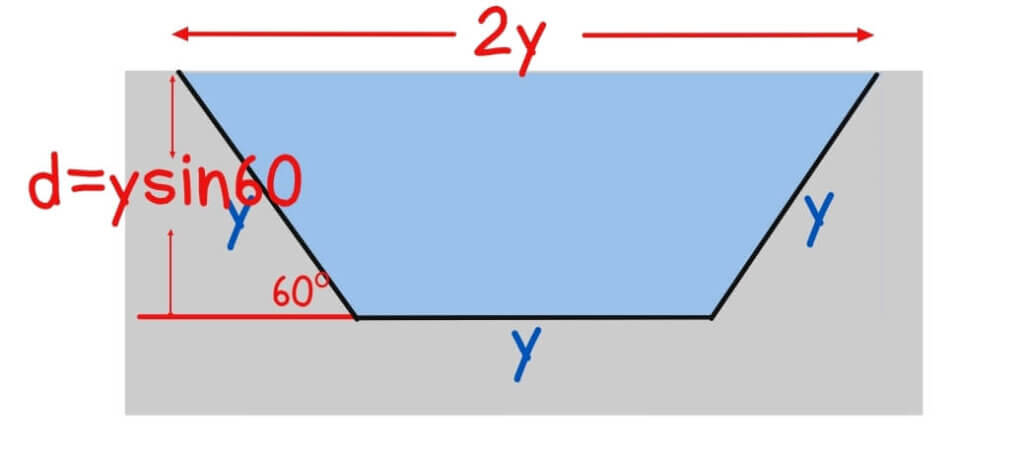
For a trapezoidal channel with bottom width b, top width B, depth d, and side slope angle θ:=

$\frac{b+B}{2}d$

For a trapezoid with specific side slopes (e.g., 60°):

$A=\frac{y+2y}{2}(ysin60^o)$

$A=\frac{3y^2\sqrt{3}}{4}$

Simplified Efficiency Formula

For the most efficient trapezoidal section (half-hexagon), the relationships can be expressed in simplified form:

$A = 1.30y^2$

$P=3y$

$R=\frac{A}{P}=\frac{1.30y^2}{3y}=0.433y$

Where y is the depth of flow. These simplified formulas are particularly useful for quick calculations in design, showing that:

The area is approximately 1.3 times the square of the depth
The wetted perimeter is exactly 3 times the depth
The hydraulic radius is approximately 43.3% of the depth

4. Semi-Circle Section

Area:

$A=\frac{\pi r^}{2}$

Perimeter:

$P=\pi r$

Hydraulic Radius
Inserting the area and perimeter to the hydraulic radius equation, we get:

$R= frac{A}{P}=\frac{\pi r^/2}{\pi r}=\frac{r}{2}$

Practical Applications

Ranking of Efficiency

From most to least efficient:

Semi-circular – Highest efficiency but difficult to construct
Trapezoidal – Excellent efficiency with practical constructability
Rectangular – Good efficiency, easy to construct with rigid materials
Triangular (45° slopes) – Lower efficiency, used for roadside ditches and small flows

Conclusion:

Understanding the most efficient hydraulic sections enables engineers to design open channels that maximize flow capacity while minimizing material costs and excavation volumes. While the semi-circular section is theoretically optimal, practical considerations often favor trapezoidal or rectangular designs. The choice of section depends on balancing hydraulic efficiency with construction feasibility, maintenance requirements, and economic constraints.

The key principle remains: minimize the wetted perimeter for a given cross-sectional area to achieve maximum hydraulic efficiency.

📍This post is part of FLUID MECHANICS COMPLETE Lessons. Also, if you want to avail the complete Cheat Sheet just click the “shop now” below.

Fluid Mechanics and Hydraulics Cheat Sheet

Master the fundamentals of fluid mechanics with this complete Fluid Mechanics Cheat Sheet designed for civil engineering students and exam reviewers. This digital guide summarizes the most important formulas, concepts, and equations. Not only it is aesthetic but also categorized by topics.

$5.00

Shop now