Forces on Vanes in Hydraulic Engineering

Understanding the forces exerted by flowing fluids on vanes is fundamental to hydraulic engineering. Whether you’re designing turbines, pumps, or analyzing jet deflection systems, the principles remain consistent: fluid momentum changes result in forces. This blog post explores the mathematical framework for calculating these hydrodynamic forces using two complementary approaches.

What you’ll learn

The Physics Foundation: Understanding Forces on Vanes

When a fluid jet strikes a vane (a curved or flat blade), it changes direction and velocity. This change in momentum must be accompanied by a force, according to Newton’s laws of motion. The beauty of this analysis lies in its versatility. We can approach it from either Newton’s Second Law or Newton’s Third Law, and both yield consistent results.

Approach 1: Newton’s Second Law

$F_{net}=R=ma$

We know that acceleration is the rate of change of velocity:

$a=\frac{V_2-V_1}{t}$

Substituing this into out force equation:

$R=\frac{m}{t}(V_2-V_1)$

Here’s where hydraulic engineering elegance emerges. The term m/t represents the mass flow rate, which can be expressed as ρQ, where ρ is fluid density and Q is volumetric flow rate. This gives us:

$\frac{m}{t}=\rhoQ$

$\rho Q(\vec{v}_2-\vec{v}_1)$

Approach 2: Newton’s Third Law (Action-Reaction)

There’s another way to look at this that many people find easier to understand. It uses the idea that impulse equals change in momentum:

$Ft= \Delta mv$

Where:
$Ft = Impulse$
$mv = momentum$

Dividing both sides by time:

$\frac{Ft}{t}=\frac{mv_1-mv_2}{t}$

This simplifies to:

$F=\frac{m}{t}(\vec{v}_1-\vec{v}_2)$

Again recognizing that m/t = ρQ:

$F_{HD}=\rhoQ(\vec{v}_1-\vec{v}_2)$

Notice the sign difference from Approach 1. This force, FHD, represents the hydrodynamic force exerted by the fluid on the vane (action-reaction pair). This is typically what engineers want to calculate when designing vane systems.

Component-Wise Analysis

In practical applications, we rarely deal with forces in a single direction. Fluid jets strike vanes at angles, and vanes deflect flow through complex curves. Therefore, we decompose the force into orthogonal components:

Forces on Vanes in Hydraulic Engineering

$F_{HD}=\rhoQ(\vec{v}_1-\vec{v}_2)$

$F_{HDx}=\rhoQ(\vec{v}_{1x}-\vec{v}_{2x})$

$F_{HDy}=\rhoQ(\vec{v}_{1y}-\vec{v}_{2y})$

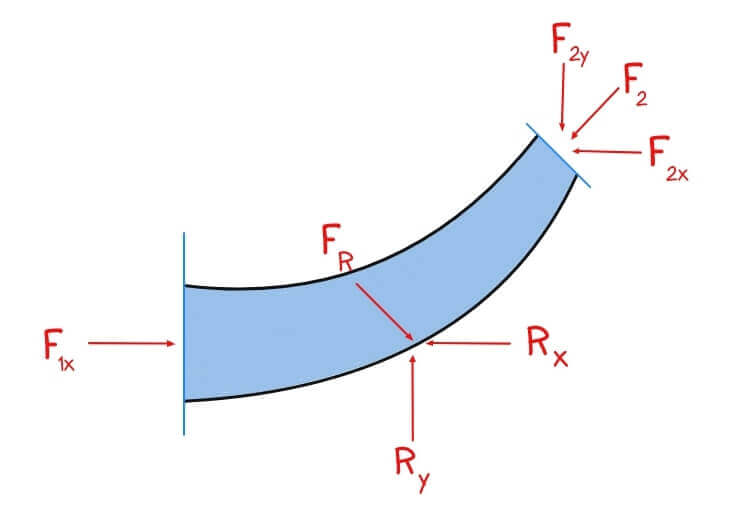
Practical Applications

Pelton Turbines: Jets strike curved buckets, and the force calculations determine power output
Reversers and Deflectors: Aircraft thrust reversers and water jet deflection systems
Pump Impellers: Understanding forces on rotating vanes helps predict mechanical stresses
Fire Hoses and Nozzles: Calculating reaction forces for safe handling

Conclusion

The force on a vane due to fluid flow is elegantly captured by the equation:

$F_{HD}=\rhoQ(\vec{v}_1-\vec{v}_2)$

This relationship, derived from fundamental Newtonian mechanics, provides hydraulic engineers with a powerful tool for analysis and design. Whether you’re calculating the thrust from a water jet or designing the next generation of hydraulic turbines, these principles remain your foundation.

References:

Crowe, C. T., Elger, D. F., Williams, B. C., & Roberson, J. A. (2009). Engineering fluid mechanics (9th ed.).

John Wiley & Sons.Munson, B. R., Young, D. F., Okiishi, T. H., & Huebsch, W. W. (2013). Fundamentals of fluid mechanics (7th ed.).

John Wiley & Sons.White, F. M. (2015). Fluid mechanics (8th ed.). McGraw-Hill Education.

📍This post is part of FLUID MECHANICS COMPLETE Lessons. Also, if you want to avail the complete Cheat Sheet just click the “shop now” below.

Fluid Mechanics and Hydraulics Cheat Sheet

Master the fundamentals of fluid mechanics with this complete Fluid Mechanics Cheat Sheet designed for civil engineering students and exam reviewers. This digital guide summarizes the most important formulas, concepts, and equations. Not only it is aesthetic but also categorized by topics.

$5.00

Shop now

CH 18: WATER HAMMER