Braced Cuts in Geotechnical Engineering Explained CEHub

Braced Cuts in Geotechnical Engineering

What you’ll learn

What is Braced Cuts in Geotechnical Engineering?

A braced cut is a temporary or permanent vertical excavation support system that consists of vertical or near-vertical walls (typically sheet piles, soldier piles, or concrete walls) held in place by horizontal structural members called struts or braces.

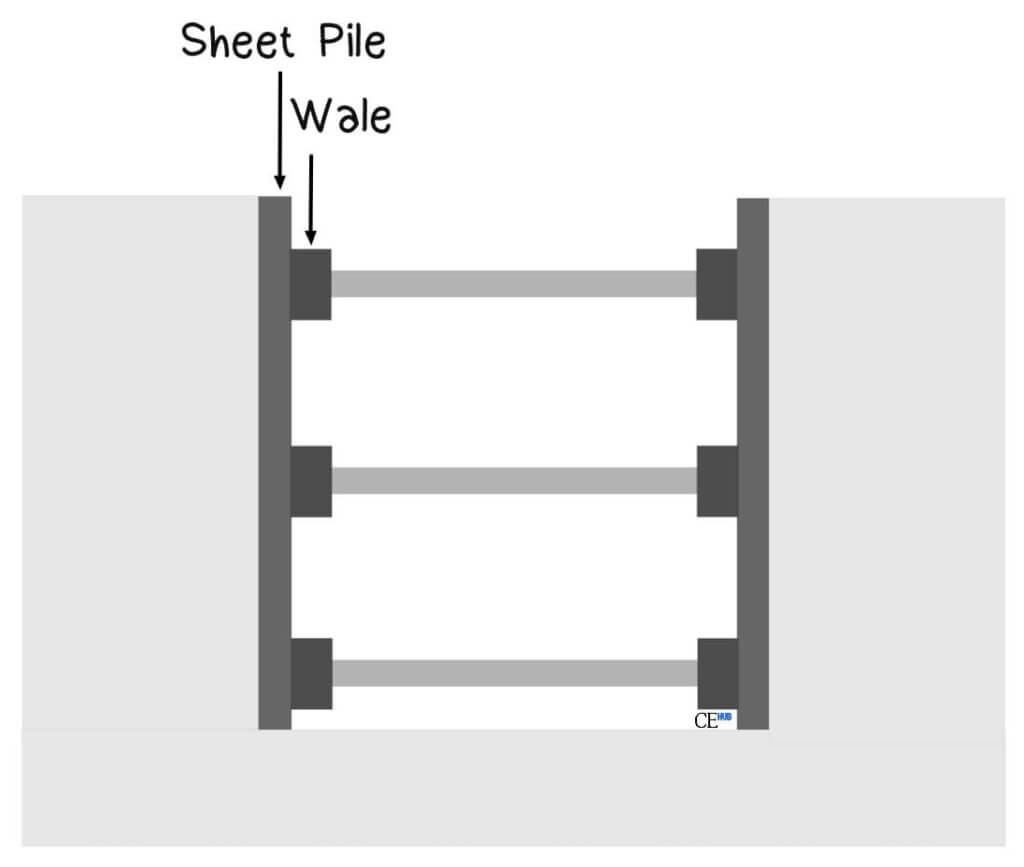
Types of Braced Cut Systems

1. Steel Sheet Pile Systems

Steel sheet piles are interlocking steel sections driven into the ground to form a continuous wall. They are particularly effective in cohesive soils and areas with high groundwater levels.

Pros:

Water retention capabilities
Suitable for various soil conditions
Provides continuous support

Cons

Limited depth capabilities in hard soils
May cause vibrations during installations
Intensive Labor

2. Soldier Pile and Lagging Systems

This system consists of steel H-piles or wide-flange beams (soldier piles) installed at regular intervals with horizontal timber or concrete lagging placed between them as excavation proceeds.

Pros

Cost-effective for moderate depths
Good visibility of soil during excavation
Flexible installation sequence

Cons

Limited water retention
Need stable soil conditions
Intensive labor

3. Diaphragm Walls

Reinforced concrete diaphragm walls are constructed in place before excavation begins. These permanent or semi-permanent structures provide excellent structural capacity and water retention.

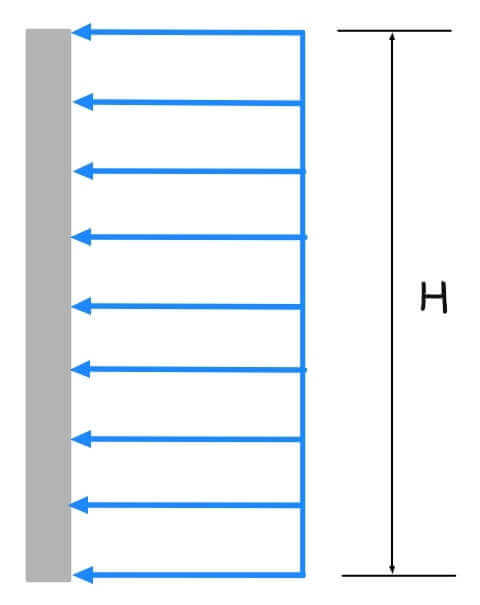
Earth Pressure for Braced Cuts

Rankine Active Pressure for Reference

For a cohesionless backfill with friction angle $\varphi$ and unit weight $\gamma$ :

$K_a=tan^2 \left( 45^o - \frac{\varphi}{2} \right$

$K_a=\frac{1-sin \varphi}{1+sin \varphi}$

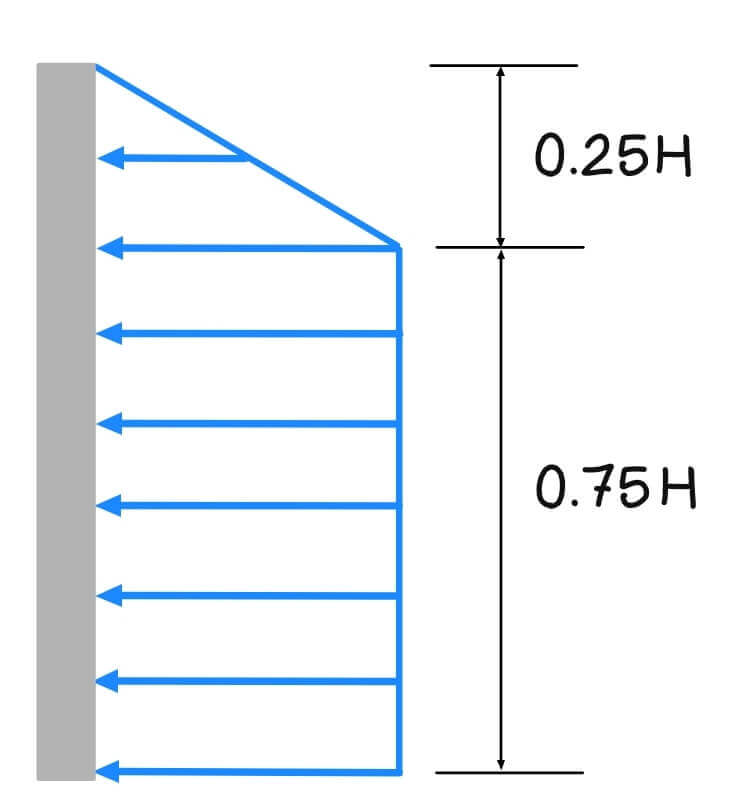
For Sands,

Peck (1969) provided the envelope of apparent-lateral pressure diagrams for design of cuts in sand. This enveloped is illustrated in figure 1

Apparent lateral pressure for cuts in sand

$\sigma_a=0.65K_a \gamma H$

where:

$\gamma$ = unit weight
$H$ = height of the cut
$K_a$ = Rankine active pressure coefficient = $tan^2(45-\phi'/2)$
$\phi'$ = effective friction angle of sand

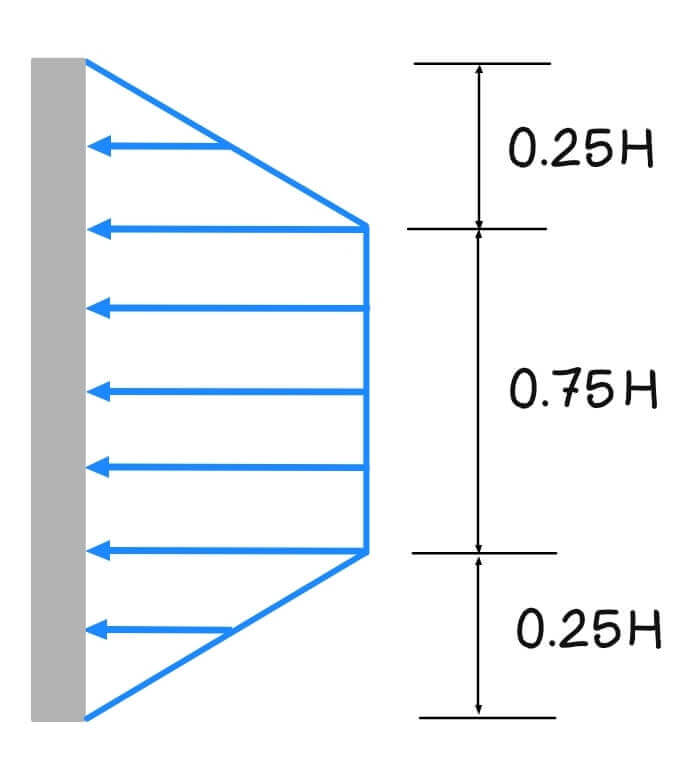
For Clays:

Peck (1969) also provided the envelopes of apparent-lateral pressure diagrams for design of cuts in soft to medium clay and stiff clay.

Soft to medium Clay

$\frac{\gamma H}{c}>4$

where:
c = undrained cohesion $(\phi=0)$

Apparent lateral pressure for cuts in clays

or (which is larger)

Stiff Clay

$\sigma_a=0.2\gamma H \: to \: 0.4\gamma H$

Pressure Envelopes on Cuts in Layered Soils

Layers of Sand and Clay

where:
$H$ = total height of the
$\gamma_c$ = unit weight of the clay
$\gamma_s$ = unit weight of the sand
$H_s$ = height of the sand
$K_s$ = lateral earth pressure coefficient for the sand layer
$\phi_s$ = effective angle of friction of
$q_u$ = unconfined compression strength of
$n'$ = a coefficient of progressive failure