Analysis of Dams in Fluid Mechanics
What is Gravity Dam?
Dams are critical infrastructural elements that serve multiple purposes, from water storage and flood control to hydroelectric power generation and irrigation. Among the various types of dams, gravity dams are particularly notable for their reliance on their own weight to resist the forces exerted by the water they hold back. In this article, we’ll delve into how gravity dams function, the physical forces acting on them, and the engineering methods used to maintain their stability and integrity.
Therefore, understanding the Analysis of Dams in Fluid Mechanics is crucial for engineers and designers so lets dig deep.
1. Hydrostatic Force
As the upstream water level rises, it exerts a horizontal hydrostatic force on the dam’s vertical face. This force increases with depth and acts perpendicular to the surface of the dam. It has two primary effects:
- Sliding tendency: The water tries to push the dam downstream.
- Overturning tendency: The pressure creates a moment that attempts to rotate the dam about its downstream edge or toe.
2. Uplift Pressure
Water doesn’t just chill upstream; there’s water underneath, which engineers in the past neglected to account for in their calculations, which led to dam failures. That pressure underneath (aka uplift force) is like a cunning little gremlin, attempting to jack the dam up and interfere with its footing. The more water seeping through, the less grip the dam has.
3. Weight of the Dam
Their weight is where gravity dams flex. They are incredibly heavy. Their entire operation revolves around that bulk. Most of its weight presses the dam into the ground, counteracting all those toppling and sliding tendencies. It is preferable if it is chunkier.
4. Frictional Resistance
There is a lot of invisible work being done by straight-up friction between the earth and the base of the dam. The more friction there is, the less likely that the entire object would skate downstream.
5. Earthquake Forces (in seismic zones)
In unstable regions, earthquake forces also need to be calculated to withstand abrupt shocks and jolts, both up and sideways, especially if it is located in a rumbling area.
Stability Considerations in Gravity Dam Design
To ensure that a gravity dam remains stable over its service life, engineers must evaluate it against three primary modes of failure:
1. Sliding
Sliding is pretty much what it sounds like; the dam tries to just slide sideways when too much water pressure pushes it. To stop it from sliding, engineers make the base super wide, which increases friction.
2. Overturning
Overturning is like the water trying to tip the dam. Because there’s a water pressure acting on the dam, therefore, we need to ensure the resisting moment is greater than the overturning moment. This is checked with a factor of safety with a value of 1.5 or more.
3. Uplfit Failure
Water doesn’t just chill upstream; there’s water underneath, and in that water–there is an uplfit pressure. If we neglect the uplift pressure in the overall calculations, failure will occur.
How to analyze a Gravity Dam?
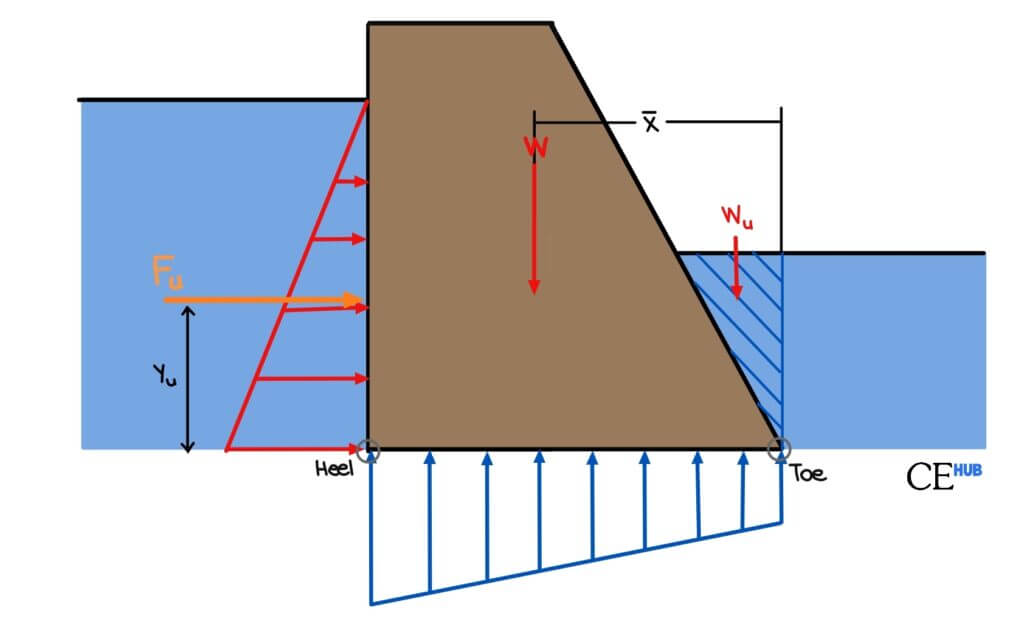
Step 1: Determine the Forces acting on the Dam
Vertical Forces
W = Weight of the Dams
Fv = Weight of water (upstream or downstream)
U = hydrostatic lift
Horizontal Forces
Fh = Hydrostatic Forces
Others (such as wind pressure, wave action, earthquake load)
Step 2: Solve for Reactions
Vertical
![]()
Sum all vertical forces. Weight of dam and water act downward (positive), uplift acts upward (negative).
![]()
Horizontal
![]()
Sum all horizontal forces. Water pressure pushes downstream (positive).
![]()
Note that if there is also water on the other side, you must also solve it and make it negative.
Step 3: Moment about the Toe
Choose a point to sum moments, conventionally the toe (downstream edge of base). This lets you find where the resultant force intersects the base.
Righting Moments (RM)
Dam weight × horizontal distance from toe to center of gravity
Water weight on upstream face × horizontal distance from toe
Any other stabilizing moments
Overturning Moments (OM): Moments that promote overturning (counterclockwise about toe)
Uplift × distance from toe to centroid of uplift distribution (typically B/3 from heel)
Hydrostatic force × vertical distance from base to its point of application (typically h/3)
Step 4. Location of Ry
Varignon’s Theorem (also called the Principle of Moments). This theorem states that the moment created by a resultant force about any point equals the sum of moments created by all the individual forces about that same point.
Think of it this way: instead of dealing with multiple forces acting at different locations on the dam (weight here, water pressure there, uplift somewhere else), we can replace them all with a single resultant reaction force Ry. But where exactly does this single force act on the base? That’s what we’re finding.
![]()
Step 5: Determine Factors of Safety
Two critical factors of safety need checking:
Factor of Safety Against Sliding (FSs)
![]()
Factor of Safety Against Overturning (FSo)
![]()
Step 6: Foundation Pressure
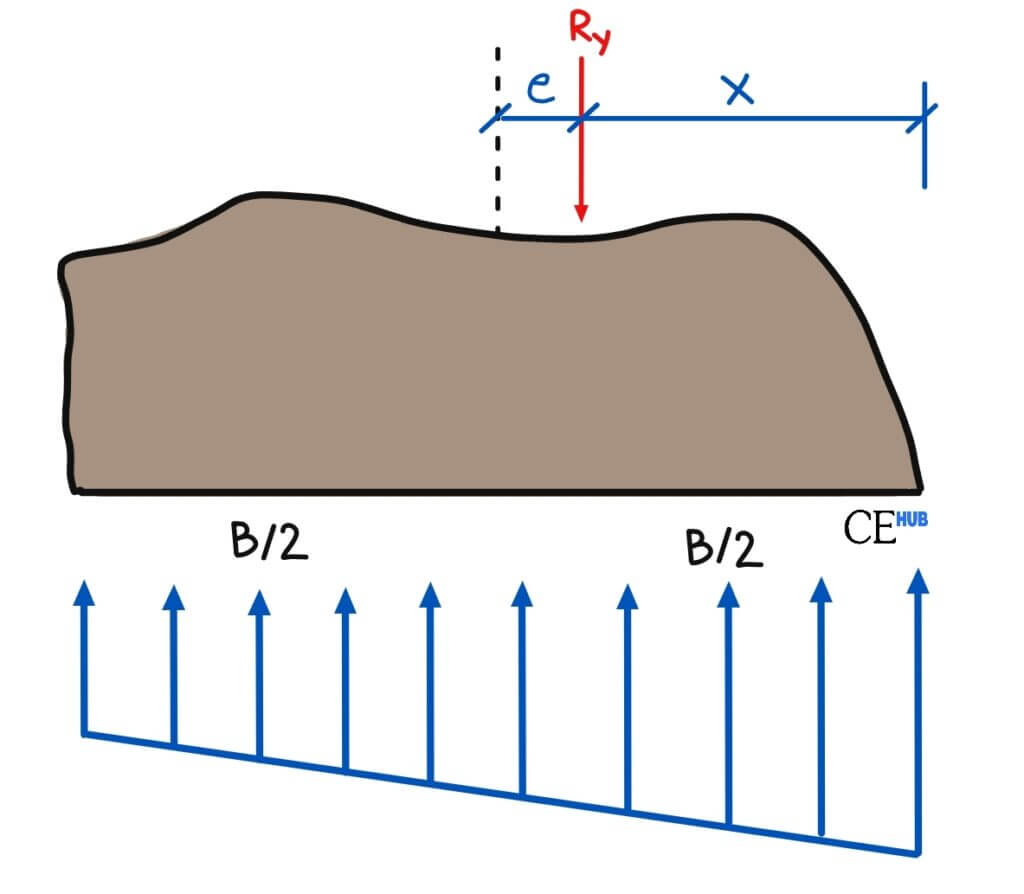
Now we check that foundation stresses don’t exceed allowable bearing capacity.
Calculate Eccentricity
![]()
Foundation Pressure Formula
The pressure distribution depends on whether e ≤ B/6 or e > B/6.
Case 1: e ≤ B/6 (Resultant within middle third)
Pressure distribution is trapezoidal with no tension:
![]()
At the toe:
![]()
At the heel:
![]()
If e = B/6 exactly, qH = 0 and you get triangular distribution.
Case 2: e > B/6 (Resultant outside middle third)
![]()
📍This post is part of FLUID MECHANICS COMPLETE Lessons please check it out to learn more of our topics.
Also, if you want to avail the complete Cheat Sheet just click the “shop now” below.

Fluid Mechanics and Hydraulics Cheat Sheet
Master the fundamentals of fluid mechanics with this complete Fluid Mechanics Cheat Sheet designed for civil engineering students and exam reviewers. This digital guide summarizes the most important formulas, concepts, and equations. Not only it is aesthetic but also categorized by topics.
Examples
EXAMPLE 1.0
The specific gravity of concrete is 2.4 and the coefficient of friction between the base of the dam and the foundation is 0.4. Use 1.5 as the factor of safety against sliding.
a) Find the width b of the concrete dam necessary to prevent the dam from sliding.
b) Is the dam safe from overturning?
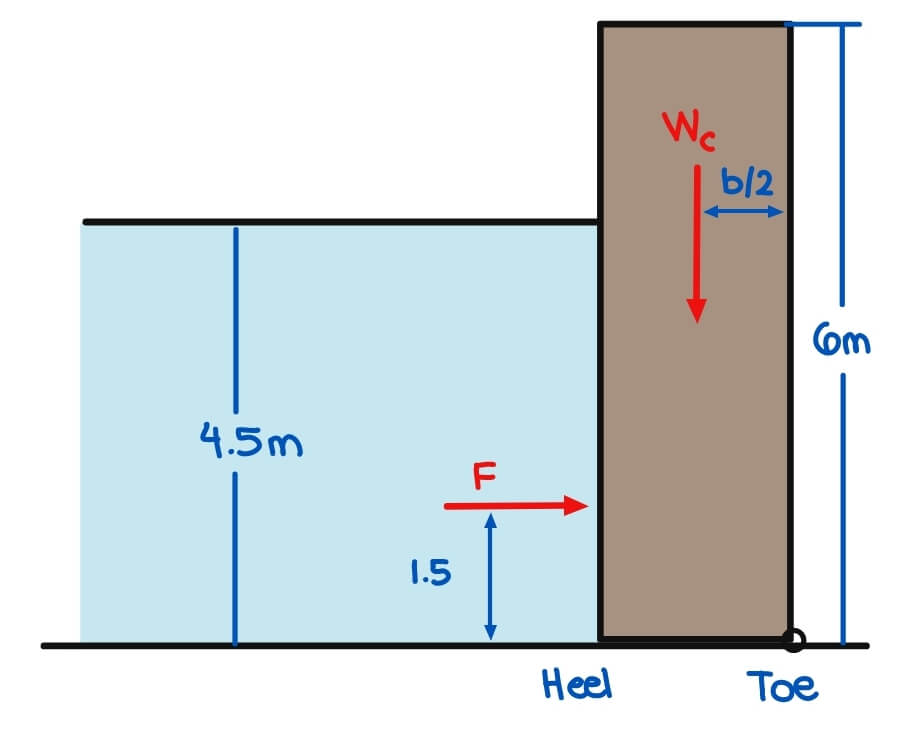
1. Determine the forces acting on it and solve for their reactions
Vertical Forces, Ry
Horizontal Forces, Rx
2. To get the b, we can use the Factor of Safety against Sliding
3. Find the factor of Safety against overturning
RM:
OM:
EXAMPLE 2.0
The dam is 9m high and 6m wide at the base and weighs 2.4 tons per cubic meter. The dam is triangular in cross-section with the upstream face vertical. The coefficient of friction between the base and the foundation is 0.9.
a) factors of safety against overturning and against sliding
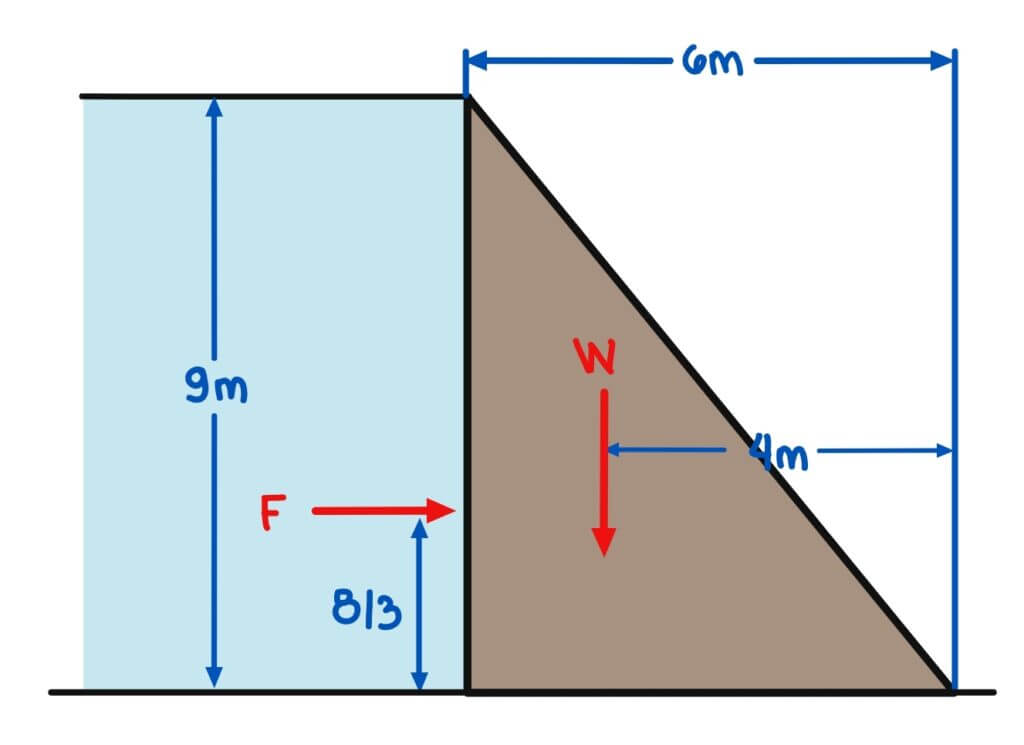
1. Determine the forces acting on it and solve for their reactions
Vertical Forces, Ry
Horizontal Forces, Rx
2. Factor of Safety against Sliding
3. Find the factor of Safety against overturning
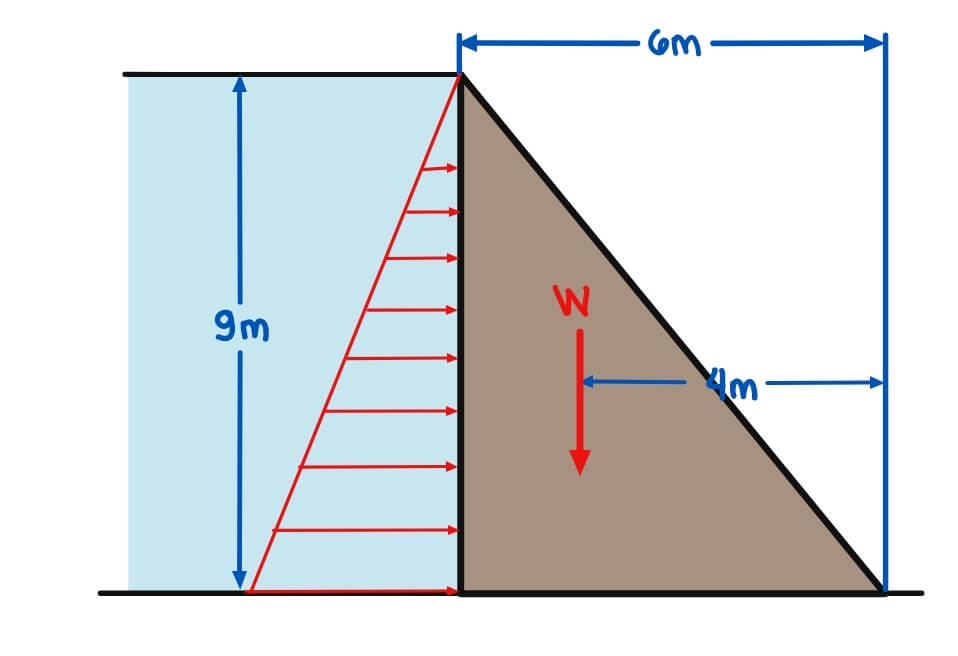
RM:
OM:







