Understanding the Bernoulli Equation In Fluid Mechanics

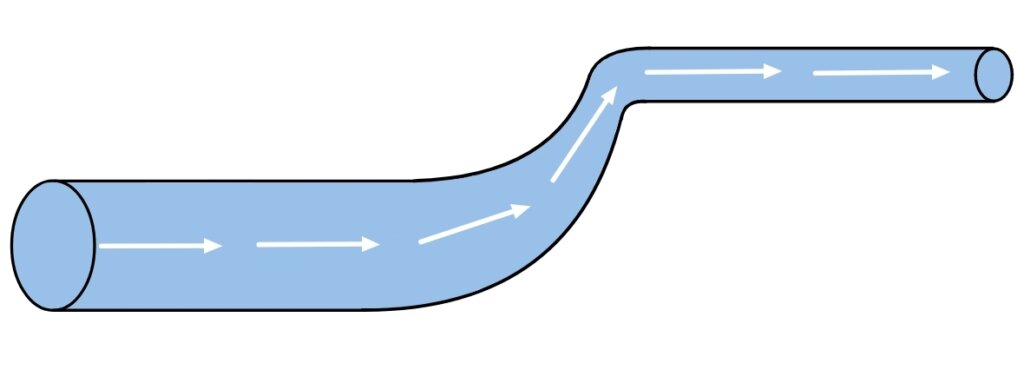
What is Bernoulli’s Equation?

DEFINITION
The Bernoulli Equation states that in a steady, incompressible, and frictionless flow, the total mechanical energy of the fluid remains constant along a streamline.
It is based on the Law Conservation of Energy where it states that “Energy cannot be created or destroyed—only transferred.“

In essence, Bernoulli’s Equation describes how pressure energy, kinetic energy, and potential energy interact within a flowing fluid system. As fluid moves through different sections of a pipe or channel, these energy forms convert into one another while maintaining a constant total energy (assuming no losses).

Why this Matter to you as a Beginner

Think of Bernoulli’s Equation as the “golden rule” of fluid mechanics, it’s one of foundation for understanding energy trade-offs in any fluid system. Here’s what makes it so powerful:

Understanding the Bernoulli Equation In Fluid Mechanics is essential for anyone studying fluid dynamics.

It Explains the Pressure-Velocity Relationship:

When water speeds up (high velocity), pressure drops
When water slows down (low velocity), pressure rises

It Connects Three Types of Energy:

Pressure energy (P/γ): The force pushing water through pipes
Kinetic energy (v²/2g): The motion of water flowing
Potential energy (z): The height advantage of the elevated tank

So in this topic, I’ll walk you through in of the most fundamental topic of Fluid Mechanics.

What you’ll learn

Historical Context

The equation is named after Swiss mathematician Daniel Bernoulli, who published it in his 1738 work “Hydrodynamica.” However, it was later derived more rigorously by Leonhard Euler using his equations of motion. This principle has since become indispensable in hydraulic engineering, aerodynamics, and various fluid mechanics applications.

Background Derivation

Bernoulli’s equation is derived from Euler’s Equation of Motion along a streamline under a steady incompressible flow.

$\frac{dP}{\rho} + gdz+ \upsilondv = 0$

Where:
= Density of the fluid (kg/m³)
= Change in elevation (m)
= Change in velocity (m/s)
= Change in pressure (N/m²)

Step 1: Integrate the Equation

$\int\left(\frac{dP}{\rho}+gdz+vdv=0\right)$

This yields:

$\frac{P}{\rho}+gz+\frac{v^2}{2}=C$

Step 2: Divide by Gravitational Acceleration (g)

$\frac{P}{\rho}+gz+\frac{v^2}{2}=C$

$\frac{P}{\rho g}+z+\frac{v^2}{2g}=C$

Since specific weight γ = ρg, and express in terms of head. We can rewrite this as:

$\frac{P}{\gamma}+z+\frac{v^2}{2g}=C$

This is BERNOULLI’S EQUATION!

Bernoulli’s Equation Formula

The general form of the Bernoulli Equation is:

$\frac{P}{\gamma}+\frac{v^2}{2g}+z=H$

Where:

P – Pressure (Pa or N/m²)
– Specific weight of fluid N/m³
v – Flow velocity (m/s)
z – Elevation above a datum (m)
H – Total head (m)

This equation expresses energy in meters of fluid (called “head”), which makes it easy to visualize using a piezometer or manometer.

Key Components of the Equation

Term	Name	Physical Meaning
$\frac{P}{\gamma}$	Pressure Head	Energy due to fluid pressure
$\frac{v^2}{2g}$	Velocity Head	Energy due to motion (kinetic)
$z$	Elevation Head	Gravitational potential energy
$H$	Total Head	Total mechanical energy of the fluid

Modified Bernoulli Equation (With Head Loss and Pumps)

In real-world engineering application, friction exists. Therefore, it is important to consider this in the overall system by modifying the equation.

$\frac{P_1}{\gamma}+\frac{v_1^2}{2g}+z_1+h_p=\frac{P_2}{\gamma}+\frac{v_2^2}{2g}+z_2+h_L+h_t$

Term	Description
$h_L$	Head loss due to friction and fittings
$h_p$	Head added by a pump
$h_t$	Head extracted by a turbine

If you want to know more about pumps and turbines in bernoulli, check out the link.

Example : Flow between two points in a Pipe

Consider a flow between two points in a pipe. At Point 1, the pressure is 400 kPa, the velocity is 2.5 m/s, and the elevation is 12 meters. At Point 2, the velocity is 3 m/s, the elevation is 8 meters, and the pressure is unknown. There is no pump in the system, and the head loss is 2 meters. The specific weight of the fluid is given as γ = 9810 N/m³. Find pressure at point 2.

Write Bernoulli with head loss

$\frac{P_1}{\gamma}+\frac{v_1^2}{g}+z_1=\frac{P_2}{\gamma}+\frac{v_2^2}{2g}+z_2+h_L$

$\frac{400000}{9810}+\frac{2.5^2}{2 \cdot 9.81}+1=\frac{P_2}{9810}+\frac{3^2}{2 \cdot 9.81} +5 +2$

$40.77+3.125+12=\frac{P_2}{9810}+0.459+8+2$

$139.406=\frac{P_2}{9810}+10.459$

$\frac{P_2}{9810}=128.947$

$P_2=128.947 \times 9810$

$P_2=1264970 \: Pa=1264.97 \: kPa$

Bernoulli’s Equation with Correction Factor

Bernoulli’s Equation is often taught in school based on ideal fluids but if you want to major in Water Resources Engineering, it is important to know that water isn’t always idealized. In real-world engineering, the flow will be uniform (usually taught in school), laminar, and turbulent. Thererfore, I will guide you to ensure that your analysis matches the real behavioural of fluids in real-world engineering by modifying the Bernoulli Equation once again using a correction factor.

A brief summary of the Modified Bernoulli Equation with correction factor:

Where α (alpha) is the kinetic energy correction factor (also called the Coriolis coefficient).

Definition of α

$alpha=\frac{\int v^3 dA}{V^3A}$

Where:

v = local velocity at a point
V = average velocity
A = cross-sectional area

Why Correction Factors

In laminar flow, velocity is highest at the center and zero at the walls (parabolic profile). In turbulent flow, the profile is flatter but still non-uniform. The kinetic energy of the actual non-uniform flow is different from that calculated using average velocity.

Typical Values of α:

Flow Type	Velocity Profile	α\alphaα
Ideal (uniform) flow	Flat profile	1.0
Laminar pipe flow	Parabolic profile	2.0
Turbulent pipe flow	Almost flat profile	1.05–1.15

Practical Applications in Civil Engineering

Bernoulli’s Equation is not just theoretical—it’s applied daily in various civil engineering disciplines.

1. Water Distribution Systems

Engineers use Bernoulli’s equation to:

Design pipe networks with adequate pressure
Size pumps for water treatment plants
Analyze pressure drops in distribution mains
Determine optimal pipe diameters

2. Open Channel Hydraulics

Applications include:

Designing spillways and weirs
Analyzing flow over dams
Calculating discharge through sluice gates
Evaluating energy dissipation in hydraulic jumps

3. Flow Measurement

Bernoulli’s principle enables flow measurement devices:

Venturi meters: Measure flow rate by pressure difference
Orifice plates: Simple flow measurement in pipes
Pitot tubes: Measure local velocity in streams or pipes

Summary and Key Takeaways

The Bernoulli Equation is a cornerstone of fluid mechanics and an indispensable tool for civil engineers. Here are the essential points to remember:

Core Principle: Total mechanical energy (pressure + kinetic + potential) remains constant along a streamline in ideal flow
Three Forms of Energy:
- Pressure head: P/γ
- Velocity head: v²/2g
- Elevation head: z
Real-World Modifications:
- Add head loss (h_L) for friction
- Add pump head (h_p) for energy input
- Add turbine head (h_t) for energy extraction
Correction Factors: Use α for non-uniform velocity profiles, especially in laminar flow and open channels

Conclusion

The Bernoulli Equation in Fluid Mechanics plays a crucial role in Civil Engineering applications. It provides a fundamental understanding of fluid flow behavior and pressure distribution in various systems. In the real world, engineers frequently rely on the Bernoulli Equation to analyze and design hydraulic systems and structures efficiently but it is also important to know various factors affecting the behavior of Fluids.

References:

Liu, C. (2013). Schaum’s Outline of Fluid Mechanics and Hydraulics, 4th Edition. McGraw Hill Professional.

‌

📍This post is part of FLUID MECHANICS COMPLETE Lessons. Also, if you want to avail the complete fluid mechanics formulas just click the image below.

Bernoulli Equation in Fluid Mechanics and Civil Engineering with Formulas

Understanding the Bernoulli Equation In Fluid Mechanics

What is Bernoulli’s Equation?

Why this Matter to you as a Beginner

Historical Context