Pumps and Turbines
As civil engineers, we frequently encounter hydraulic systems where energy must be added to or extracted from flowing fluids. Understanding how pumps and turbines interact with the Bernoulli Energy Equation is fundamental to designing water supply systems, hydroelectric facilities, irrigation networks, and drainage infrastructure.
If you want to learn Bernoulli Energy Equation Fundamentals first you can click the link.
Understanding Pumps vs Turbines in Fluid Systems
Pumps
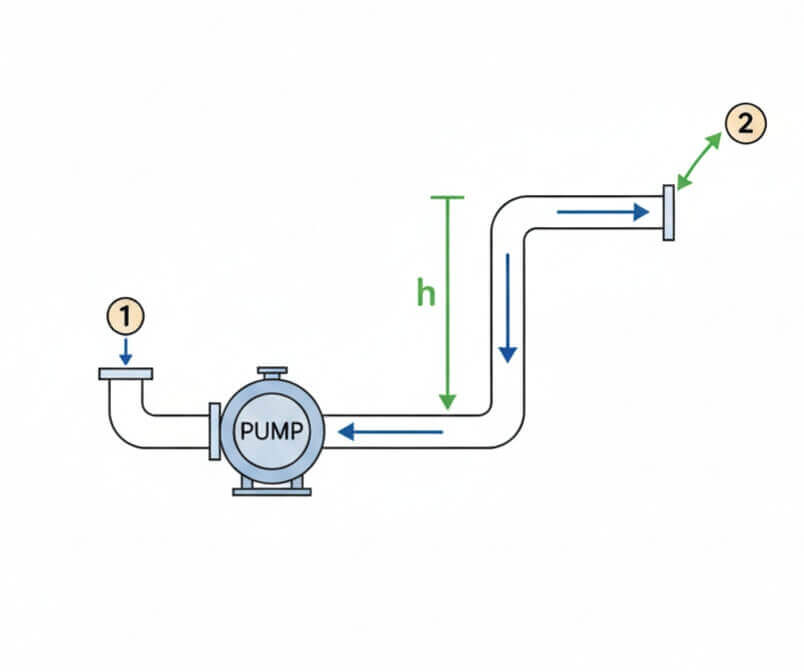
Pumps are mechanical devices that add energy to a fluid system. They work by converting mechanical energy (typically from an electric motor or engine) into hydraulic energy, which increases the total energy of the fluid.
This energy addition allows water to:
- Flow uphill against gravity
- Increase pressure in a system
- Maintain flow rates
Turbines
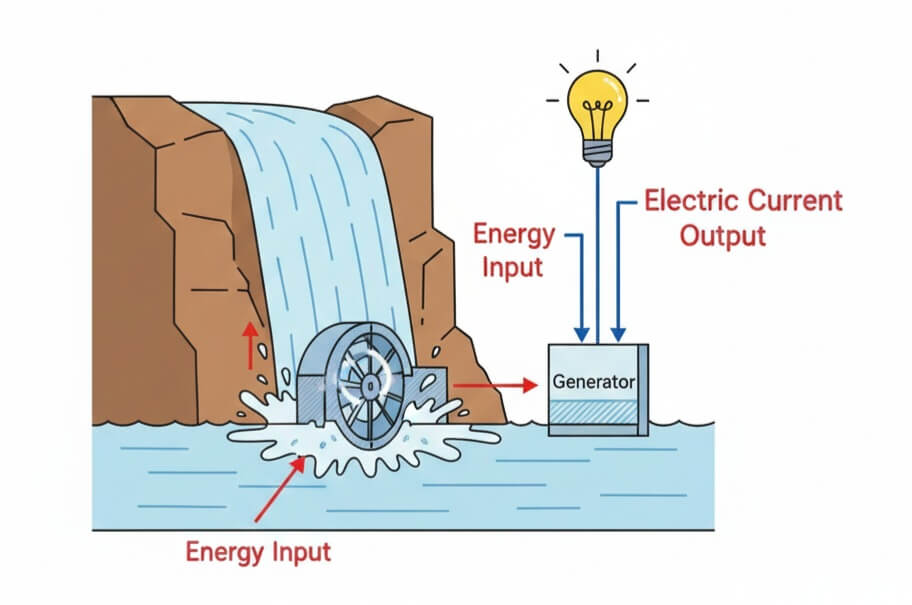
Turbines perform the opposite function of pumps, they extract energy from flowing fluid and convert it into mechanical work, typically to generate electricity. The fluid does work on the turbine blades, causing rotation that drives a generator.
This energy is critical in:
- renewable energy generation
- pump storage facilities
The Bernoulli Energy Equation
The original equation was:
![]()
When a pump is present in a fluid system, we modify the standard Bernoulli equation to account for the energy added. The equation becomes:
![]()
When it is turbine,
![]()
Where:
P/γ = Pressure head
v²/2g = Velocity head
z = Elevation head
HA = Head added by the pump
HE = Head extracted by the turbine
Power
Power is different from energy.
- Energy is the capacity to do work (measured in Joules or Newton-meters)
- Power is the rate at which energy is transferred or work is done (measured in Watts or Joules per second)
In hydraulics, we express energy per unit weight, which gives us units of length (meters or feet). This is why pump and turbine performance is described in terms of “head” rather than total energy.
Power Units in Engineering
- 1 Watt = 1 Joule/second = 1 N·m/s
- 1 Horsepower (HP) = 746 Watts
- 1 HP = 0.746 kW
- 1 HP = 550 ft·lbf/s (US customary)
![]()
Where:
P = Power
Q = Flow Rate
γ = Specific weight of fluid
H = Head added (H_A) or extracted (H_E) in meters
Efficiency
Not all machines are perfect. Some machines experiences friction in bearings and seals, turbulence, leakage, electrical losses, etc. That’s why we compute efficiency of the machine:
![]()
For Pumps
- P_in = Electrical or mechanical power supplied to the pump
- P_out = Hydraulic power delivered to the fluid
- Typical efficiencies: 60-85% for centrifugal pumps, 70-90% for positive displacement pumps
For Turbines
- P_in = Hydraulic power available from the flowing fluid
- P_out = Mechanical/electrical power generated
- Typical efficiencies: 85-95% for large hydro turbines
Engineering Applications
Pump Applications in Civil Engineering
- Municipal water distribution systems
- Wastewater treatment plant operations
- Stormwater management and flood control
- Irrigation and agricultural water delivery
- Building HVAC and plumbing systems
Turbine Applications in Civil Engineering
- Hydroelectric power generation at dams
- Small-scale hydro projects in water distribution systems (energy recovery)
- Pumped storage facilities
- Industrial process water energy recovery
Conclusion:
Understanding how pumps and turbines interact with the Bernoulli Energy Equation is essential for civil engineers working with fluid systems. Pumps add energy (represented by +H_A), turbines extract energy (represented by -H_E), and real machines always operate with less than 100% efficiency.
The distinction between energy and power, combined with proper application of the modified Bernoulli equation, allows engineers to properly size equipment, predict system performance, and design efficient hydraulic infrastructure.
Remember that in real-world applications, you must always account for friction losses, minor losses at fittings, and equipment efficiencies to produce accurate and reliable designs. The theoretical equations provide the foundation, but engineering judgment and experience turn theory into successful infrastructure.
📍This post is part of FLUID MECHANICS COMPLETE Lessons. Also, if you want to avail the complete Cheat Sheet just click the “shop now” below.

Fluid Mechanics and Hydraulics Cheat Sheet
Master the fundamentals of fluid mechanics with this complete Fluid Mechanics Cheat Sheet designed for civil engineering students and exam reviewers. This digital guide summarizes the most important formulas, concepts, and equations. Not only it is aesthetic but also categorized by topics.



