Hydrostatic Forces on Plain and Curved Surfaces
What you’ll learn
Hydrostatics provides fundamental insights key to some aspects of fluid mechanics, particularly in understanding Fluid Mechanics equations. Static fluids exert force on any submerged surface, and grasping this concept is crucial in the field of hydrostatics. In particular, professionals in civil and hydraulic engineering focus on these forces while constructing structures such as dams, gate systems, and large containment tanks.
What are Hydrostatic Forces?
Hydrostatic Forces arise from the pressure exerted by a fluid at rest. It occurs when the fluid is stationary relative to the surface it contacts.
Hydrostatic Forces on Plain Surfaces
The pressure in a static fluid increases linearly with depth due to the weight of the fluid column above any given point.
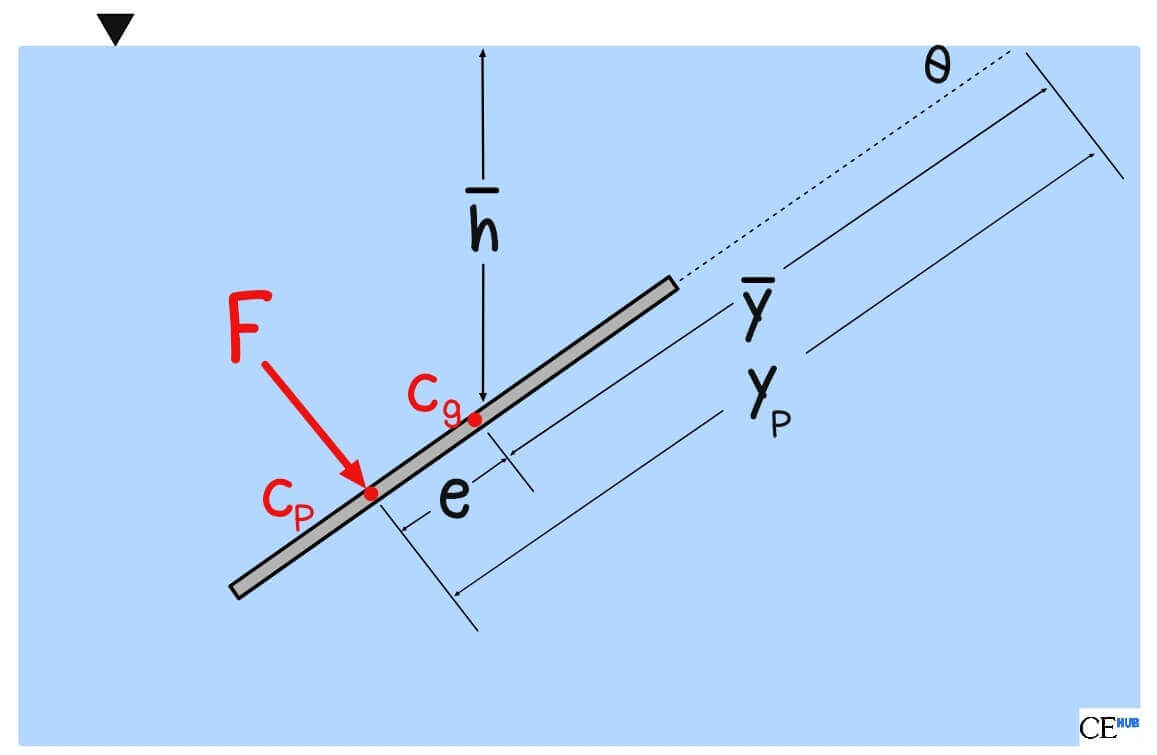
Fluids exert pressure on submerged surfaces, resulting in an upward force acting on them. This Force is due to the net fluid pressure acting on a submerged surface and this force can be written as:
![]()
For a uniform liquid at rest, the equation can be rewritten using the liquid’s unit weight:
![]()
where:
F = force on the plate
= depth of the centroid of the surface from the free surface
= specific weight of the liquid
A = submerged area of the plate
Location of the Center of Pressure
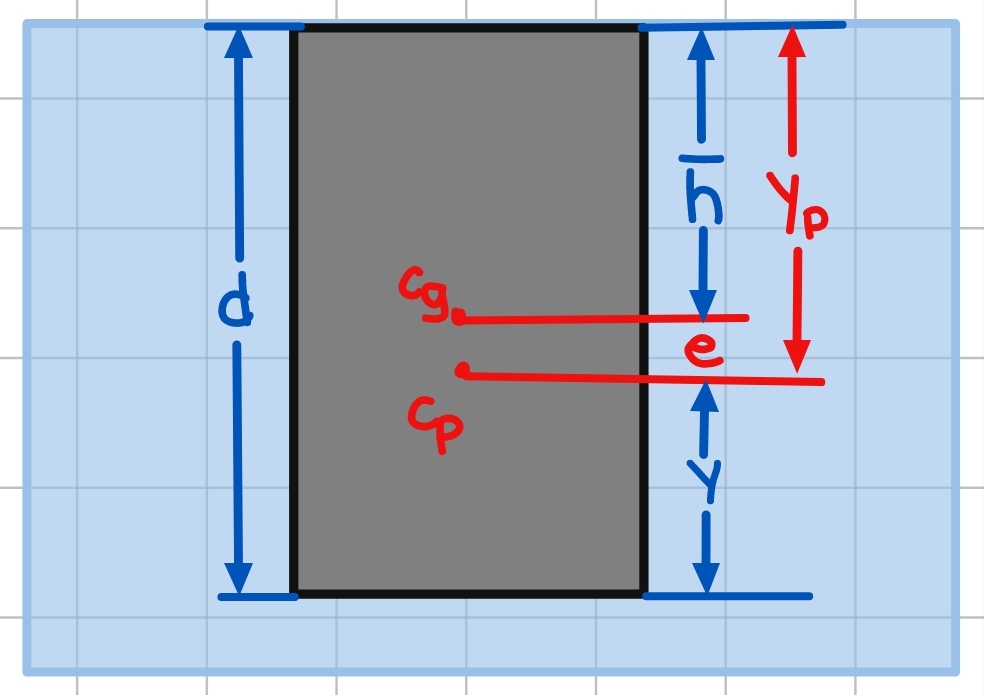
The resulting force position can be defined by the center of pressure (CoP) which denotes the location where the resultant force acts. As a result of the increase in pressure at a greater depth, the center of pressure is always lower than the center of gravity.
![]()
where e:
![]()
Ig is the moment of inertia of the surface about its own centroidal axis.
A is the submerged area of the plate
ӯ is the depth of the centroid
Since e is always positive, this means that hp > hg meaning the center of pressure is always below the centroid of the surface.
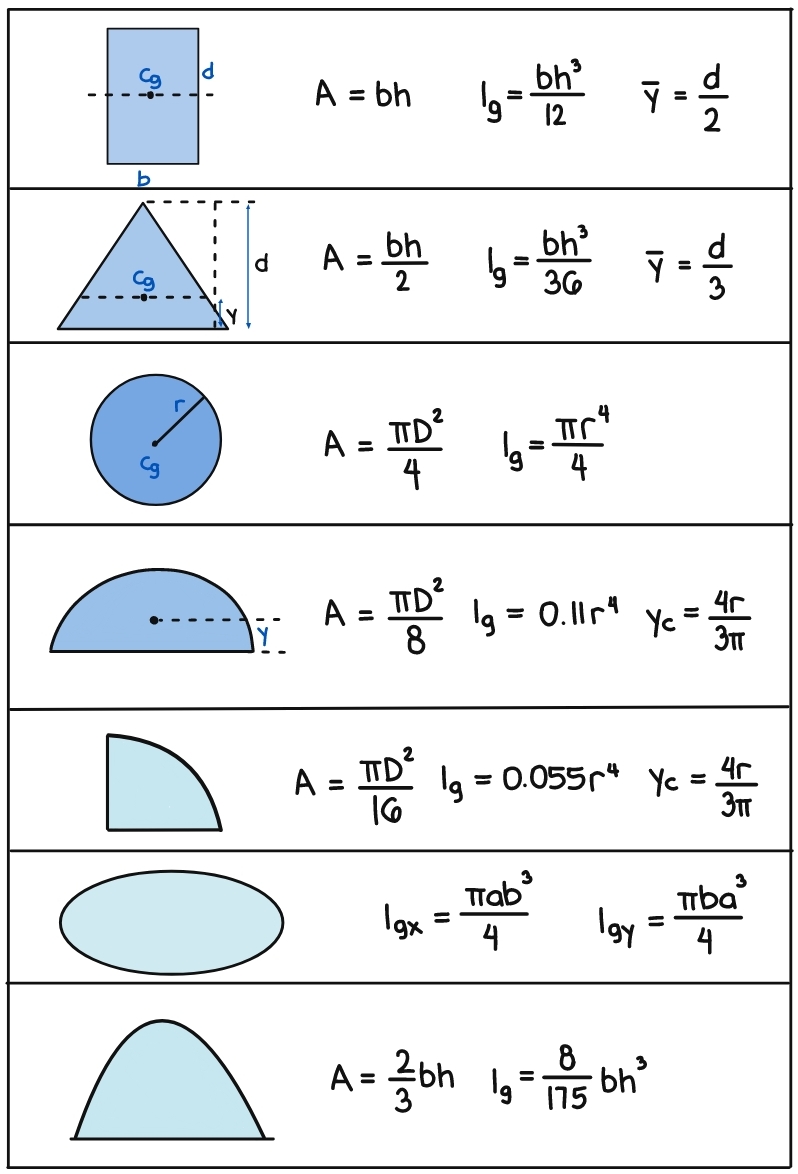
Moment of Inertia along the Neutral Axis
It is essential to know some basic plane section to locate the depth of the centroid of a section. Here’s some properties of common plane section:
Hydrostatic Forces on Curved Surfaces
The hydrostatic forces acting on a submerged curved surface can be broken down into two components: horizontal and vertical. These forces arise from the pressure exerted by the fluid and always act perpendicular to the surface.
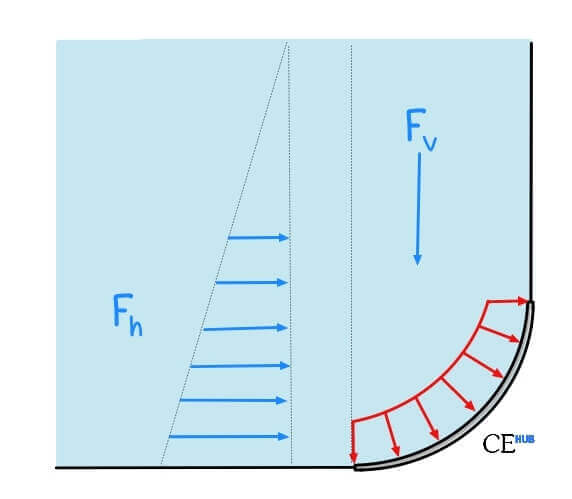
Step 1: Compute the Horizontal Force
![]()
Step 2: Compute the Vertical Force
This equals the weight of the fluid directly above the surface and is determined based on the fluid’s density and volume.
![]()
Step 3 Compute the Resultant Hydrostatic Force
The Total hydrostatic force on the curved surface can be obtained by combining the horizontal and vertical force components.
![]()
Fluid Mechanics Cheat Sheets
Struggling to recall the formulas for Bernoulli’s Equation, Hydrostatic Pressure, or Flow Rate?
Download my Fluid Mechanics Cheat Sheet for Civil Engineers — your ultimate cheat sheet – a complete formula notes for your exams.

Sample Problems
References:
Evett, J. B., & Liu, C. (1994). 2500 Solved Problems in Fluid Mechanics and Hydraulics.
Gillesania. Fluid Mechanics and Hydraulics 4th Edition
Next: Dams






